Part of my research interests is in statistical mechanics-the study of how the physical properties of matter are governed by the statistical properties of single or ensemble collections of atoms and molecules.  

     I suppose, then, it is no coincidence that when I began work on how humor is processed in the brain that the statistical properties of language might become important in the analysis.  Indeed, humor (at least in the theory I am developing) is a statistical inference process that leads to a bifurcation in meaning at the punchline.  I may present that theory in more detail in another post, since it is complicated, but in this post, I want to talk about one of the useful tools in studying the statistical properties of language or, more specifically, word use.

     One of the interesting cathologies here is that the same theory used by computational linguistics to study the statistics of word use is virtually identical to that used by theoretical physicists and chemists to study the statistical properties of atoms and molecules in liquids.  Indeed, one could describe language as a type of liquid, with words having short-range attractions to other words.  For instance, the word cluster: Charlie Brown Lucy Running, attracts the word, football.  In biology, since the base pairs of DNA sequences may be thought of as words, the same theory may be applied to base pairs in genomes.

     In computational linguistics, an N-gram is a continuous sequence of one or more words, parts of words, or parts of pronunciation of words (phonemes, for example) in a long string of words or text.  A single word (syllable, phoneme, etc.) is called a unigram, two words forming a cluster is called a bigram, three word, a trigram, etc.  Thus, Charlie Brown and Lucy, would be a tetragram.  When the statistical object under consideration is specifically words (as opposed to other components of language), an N-gram is sometimes also called a shingle.

     In liquid-state physics, atoms or molecules have short-range attraction and so tend to form clusters (and, here).  There are various ways in which a cluster of, say, one to five molecules may combine and so the overall properties of liquids are found using the weighted sum of these different clusters (figure 1, from, Ushcats, Michael & Bulavin, Leonid & Sysoev, Vladimir & Bardik, Vitaliy & Alekseev, Alexandre. (2016). Statistical theory of condensation — Advances and challenges. Journal of Molecular Liquids. 224. 10.1016/j.molliq.2016.09.100.).

Figure 1.  Cluster formation in two to five atoms

     Unlike identical clusters of atoms in a liquid, the order in an N-gram of words is important because words have semantic meanings.  In a trigram of words, there can be various relationships between word clusters (figure 1a).

Figure 1a.  Trigram semantics

     In assigning probabilities of one word following another in N-gram clusters, the best we can do at the moment in computational linguistics is to assume that the probability of word two being followed by word one is only determined by the properties of word one, or, in some cases, the immediate n-1 words just before it, so three words are determined by the last two, etc, and not by any words that might have been used further upstream in the text.  This limitation is called the Markov Property and the chains of words in an N-gram form a Markov chain.  This means that an N-grams has a very short-term memory of what words went on before it (figure 2, a Markov chain of a trigram, from Wikimedia).

Figure 2.  A Markov chain for trigrams in a corpus.

In order to calculate probabilities, we need a sampling of words.  This reference collection of words is called a corpus.  Typically, corpuses are drawn from public domain book, articles, newspapers, etc.  There are several standard corpuses that linguists use, such as the Brown Corpus, from Brown University.

     What I want to talk about in this post is the Google Corpus, which is one of the largest in the world, containing,155 billion American, 35 billion British, and 45 billion Spanish words, from 1500 A. D. to the present.  Google has created an N-gram Viewer, which allows one to study the probability of use of a word or phrase over this time period.  It can be used for a fascinating study of word use over time and shows how history can be defined in word usage.

     Let’s take a simple example.  The laser did not exist before 1960 and when it first was invented, it was known by its acronym, LASER.  If we put the word, LASER, into the N-gram viewers we find the following graph (figure 3):

Figure 3.  The N-gram of “LASER”

It is easy to see that the word LASER began to be used in English in about 1964.  The small rise in 1979 corresponds to the advent of the Star Wars franchise.

     If one searches for, Spirit of Vatican II, one finds the following graph (figure 4):    

Figure 4.  N-gram of “The Spirit of Vatican II”

One can plainly see that the term was introduced during the Council and had its peak usage from 1966 to 1970.  What is very telling is the extreme rise in usage starting in 2006, about the time that Summorum Pontificum made the Traditional Latin Mass more available.

     The term, Traditional Latin Mass shows a similar rapid rise from the mid-2000’s, on (figure 5):

Figure 5.  N-gram of “Traditional Latin Mass”

Figure 5a.  N-grams for “Traditional Latin Mass” and “Spirit of Vatican of Vatican II”

     If one searches for Catholic Mass, one finds something very interesting (figure 6):

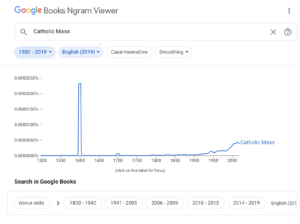
Figure 6. N-gram of “Catholic Mass”

The large spike from 1595 to 1607 or so corresponds to the severe Catholic repression of Queen Elizabeth I during the Irish Nine Years War.

The N-gram Viewer is well worth exploring for all of the parts of speech.

     One final remark: the rise of the Internet seems to have created a more selfish culture.  This is suggested by the rise in the use of the word, I, since 2000 (figure 7):

Figure 7.  The N-gram of “I”

Just something to think about…