I. Introduction

     At the blog of Fr. John Zuhlsdorf (Fr. Z’s Blog), several posts have been made regarding certain bishops restricting the reception of Holy Communion to only Communion in the hand during the COVID-19 pandemic.  One exasperated commenter wrote (I will leave out his name, since I do not know if he wants it posted):

“This entire conversation, and the fact that any bishop would even make an issue of it, centers around a premise that receiving Communion in the hand is safer, while Communion on the tongue is more dangerous. And yet, the only relevant science of which I am aware, was the discovery announced by Archbishop Alexander Sample of Portland, Oregon, that receiving on the tongue is no more dangerous than receiving in the hand.

So, where is every other bishop getting the idea that the hand is safer than the tongue? Where is the science?”

     Since there has been absolutely no scientific study on the matter (and the opinion of the two epidemiologists consulted by Bishop Sample or even 21 doctors mentioned in a recent Lifesite article [here] about an issue in an area never before studied does not count for much) and not having a lab from which to test the hypothesis, I will do what every good theorist would do: I will build models of Communion in the hand and Communion on the tongue to see if there is anything we can learn about the differences from the models.  As simple a question as this might seem, it uncovers a lot of interesting science and not a few hidden connections (cathologies) to some seemingly unrelated things.

     We will call the Priest (or the Extraordinary Minister of Holy Communion, as the case may be), the Sender, S, and the Communicant, the Receiver, R.  The methods of contact may be divided into four categories: contact with no virus, contact with virus, non-contact with no virus, and non-contact with virus.  There are three possible bodily fluid transmission routes: saliva, sweat, or aspirations.  Likewise, there are two contact areas: the tongue and the hand.  We may use the following short-hand to represent any type of contact by a nine-digit binary number, a_nb_nc_nd_ne_nf_ng_nh_ni_n, where a = Sender contact (0 = no, 1 = yes), b = Sender virus state (0 = no virus, 1 = has virus), c = tongue (0) or hand (1), d = Receiver contact (0 = no, 1 = yes), e = Receiver virus state (0 = no virus, 1 = has virus), with Virus, f = tongue (0) or hand (0), g = saliva (0 = no, 1 = yes), h = sweat (0 = no, 1 = yes), and i= aspiration (0 = no, 1 = yes).    The matrix is nothing more than the numbers 0 through 511 (= 2^9 = 512 binary states) expressed in binary:

000000000	001000000	010000000	011000000	100000000	101000000	110000000	111000000
000000001	001000001	010000001	011000001	100000001	101000001	110000001	111000001
000000010	001000010	010000010	011000010	100000010	101000010	110000010	111000010
000000011	001000011	010000011	011000011	100000011	101000011	110000011	111000011
000000100	001000100	010000100	011000100	100000100	101000100	110000100	111000100
000000101	001000101	010000101	011000101	100000101	101000101	110000101	111000101
000000110	001000110	010000110	011000110	100000110	101000110	110000110	111000110
000000111	001000111	010000111	011000111	100000111	101000111	110000111	111000111
000001000	001001000	010001000	011001000	100001000	101001000	110001000	111001000
000001001	001001001	010001001	011001001	100001001	101001001	110001001	111001001
000001010	001001010	010001010	011001010	100001010	101001010	110001010	111001010
000001011	001001011	010001011	011001011	100001011	101001011	110001011	111001011
000001100	001001100	010001100	011001100	100001100	101001100	110001100	111001100
000001101	001001101	010001101	011001101	100001101	101001101	110001101	111001101
000001110	001001110	010001110	011001110	100001110	101001110	110001110	111001110
000001111	001001111	010001111	011001111	100001111	101001111	110001111	111001111
000010000	001010000	010010000	011010000	100010000	101010000	110010000	111010000
000010001	001010001	010010001	011010001	100010001	101010001	110010001	111010001
000010010	001010010	010010010	011010010	100010010	101010010	110010010	111010010
000010011	001010011	010010011	011010011	100010011	101010011	110010011	111010011
000010100	001010100	010010100	011010100	100010100	101010100	110010100	111010100
000010101	001010101	010010101	011010101	100010101	101010101	110010101	111010101
000010110	001010110	010010110	011010110	100010110	101010110	110010110	111010110
000010111	001010111	010010111	011010111	100010111	101010111	110010111	111010111
000011000	001011000	010011000	011011000	100011000	101011000	110011000	111011000
000011001	001011001	010011001	011011001	100011001	101011001	110011001	111011001
000011010	001011010	010011010	011011010	100011010	101011010	110011010	111011010
000011011	001011011	010011011	011011011	100011011	101011011	110011011	111011011
000011100	001011100	010011100	011011100	100011100	101011100	110011100	111011100
000011101	001011101	010011101	011011101	100011101	101011101	110011101	111011101
000011110	001011110	010011110	011011110	100011110	101011110	110011110	111011110
000011111	001011111	010011111	011011111	100011111	101011111	110011111	111011111
000100000	001100000	010100000	011100000	100100000	101100000	110100000	111100000
000100001	001100001	010100001	011100001	100100001	101100001	110100001	111100001
000100010	001100010	010100010	011100010	100100010	101100010	110100010	111100010
000100011	001100011	010100011	011100011	100100011	101100011	110100011	111100011
000100100	001100100	010100100	011100100	100100100	101100100	110100100	111100100
000100101	001100101	010100101	011100101	100100101	101100101	110100101	111100101
000100110	001100110	010100110	011100110	100100110	101100110	110100110	111100110
000100111	001100111	010100111	011100111	100100111	101100111	110100111	111100111
000101000	001101000	010101000	011101000	100101000	101101000	110101000	111101000
000101001	001101001	010101001	011101001	100101001	101101001	110101001	111101001
000101010	001101010	010101010	011101010	100101010	101101010	110101010	111101010
000101011	001101011	010101011	011101011	100101011	101101011	110101011	111101011
000101100	001101100	010101100	011101100	100101100	101101100	110101100	111101100
000101101	001101101	010101101	011101101	100101101	101101101	110101101	111101101
000101110	001101110	010101110	011101110	100101110	101101110	110101110	111101110
000101111	001101111	010101111	011101111	100101111	101101111	110101111	111101111
000110000	001110000	010110000	011110000	100110000	101110000	110110000	111110000
000110001	001110001	010110001	011110001	100110001	101110001	110110001	111110001
000110010	001110010	010110010	011110010	100110010	101110010	110110010	111110010
000110011	001110011	010110011	011110011	100110011	101110011	110110011	111110011
000110100	001110100	010110100	011110100	100110100	101110100	110110100	111110100
000110101	001110101	010110101	011110101	100110101	101110101	110110101	111110101
000110110	001110110	010110110	011110110	100110110	101110110	110110110	111110110
000110111	001110111	010110111	011110111	100110111	101110111	110110111	111110111
000111000	001111000	010111000	011111000	100111000	101111000	110111000	111111000
000111001	001111001	010111001	011111001	100111001	101111001	110111001	111111001
000111010	001111010	010111010	011111010	100111010	101111010	110111010	111111010
000111011	001111011	010111011	011111011	100111011	101111011	110111011	111111011
000111100	001111100	010111100	011111100	100111100	101111100	110111100	111111100
000111101	001111101	010111101	011111101	100111101	101111101	110111101	111111101
000111110	001111110	010111110	011111110	100111110	101111110	110111110	111111110
000111111	001111111	010111111	011111111	100111111	101111111	110111111	111111111

Table 1: All Possible Interactions Between Sender and Receiver in Offering Communion

     The table is read according to the following example: 111100110 means: Sender contact, with virus, on the hand, Receiver contact, but he does not have the virus, on the tongue, the contact is with viral sweat being the transmission fluid, and non-viral saliva present:

  Thus, this is the symbolic representation of communion on the tongue with the priest having the virus passing it to the Communicant via sweat while the Communicant’s non-viral saliva is passed to the priest .  It should be clear that most of these combinations are unrealistic, in practice, however, since Communion is only given on either the tongue or the hand, but not both, so that all combinations having a 0 in both columns 3 and 6 are, automatically eliminated, for example.  It is possible to reduce the contact matrix quite substantially using these and similar arguments.

     Some of the most common types of Communion with either no virus transfer or virus transfer are summarized in table 2.

Contact Pattern	Interpretation
111101010	hand, priest has virus
111100110	tongue, priest has virus
101100000	tongue, no virus
101101000	hand, no virus
101111010	hand, communicant has virus
101110100	tongue, communicant has virus

Table 2: Realistic Cases of Virion Transfer

The four most common scenarios that people ask about are: 1) contactless Communion on the tongue, 2) Communion on the tongue with contact, 3) Communion in the hand with dry contact, 4) Communion in the hand with wet contact.  We will examine each of these.

II. Communion on the tongue, no contact

     Communion on the tongue is a more complicated process than simply depositing the Host on the Communicant’s tongue.  The tongue (figure 1, adopted from Wikimedia [1 ]) is composed of four sections comprising, roughly, the back, middle, sides, and front environments.  The papilla become gradually thinner and more raised from the back to the front.  Communion on the tongue involves only the front (filiform papilla) and middle (fungiform papilla) sections of the tongue. 

Figure 1.  Tongue architecture

       There is a seven-step process involved in reception of the Host on the tongue (figure 2, see [2 ], page 282 for a fascinating connection to atomic force microscopy ). 

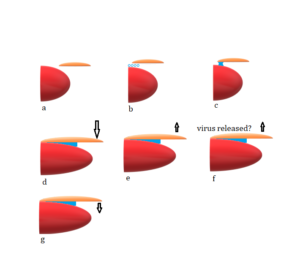
Figure 2.  Communion on the tongue

     Initially, the Host approaches the tongue from outside the mouth (a).  In the next step, the surface water and mucin molecules of saliva begin to attract the starch molecules of the Host by London forces and hydrogen bonding (b) [3].  Then, a capillary bridge of saliva begins to form between the filiform papilla and the Host surface (c).  This is called the jump-in force, because the formation of the capillary bridge is sudden and pulls the Host down towards the tongue.[2]  The formation of this capillary bridge is also responsible for the ability of certain bugs to walk vertically on surfaces.[4]  The insects secrete water between the pads of their toes allowing the formation of a capillary bridge with the wall.  The force of S’s hand is directed downward in this phase [5].  It is possible to model this capillary force as the pull between two flat plates (the Host and the tongue) or as the accumulated force between a flat plate and an n x n array of capillary tubes, modeling the fuliform papilla.  We will use the former method, here.

     This is followed by physical contact of the Host with the tongue with the formation of an elongated salival capillary bridge in the exposed interstitial region (d).  The next step is the release of the Host from S’s hand (e), which creates a small pull-back force followed by an air pressure jet as the hand is pulled away (f).[6]  The tongue is slightly bent upwards and then relaxes visco-elastically back into place.[7]

     It is possible to calculate the force of the initial capillary bridge (figure 3, adapted from Wikimedia from a sketch by Pvpetkov [8] ) using the Young-Laplace equation and treating the Host and tongue as parallel flat plates (for a description treating the individual filiform papilla, see [9]:

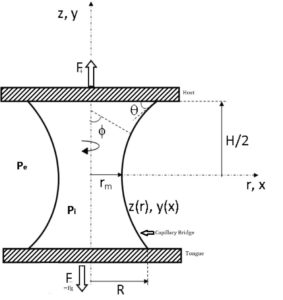
Figure 3.  Flat plate capillary bridge geometry

     Here, z, r, and ϕ are the cylindrical coordinates, θ is the contact angle, H is the height of the bridge, r_m is the minor radius (= R₁ in the Young-Laplace equation) and R is the major radius (= R₂ in the YL equation).

     In the absence of a gravitational field, the YL equation takes the form:

where γ is the surface tension and R₁ and R₂ are the radii of curvature, as defined, above.  ΔP is the pressure difference, P_internal -P_external = P_i – P_e across the boundary, as indicated in the diagram.  This is, also, equal to the attractive (in this case) capillary pressure: P_γ = ΔP, so that equation (1) takes the form:

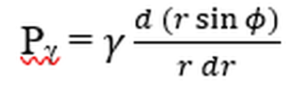
     Without reproducing the standard derivation, which may be found in [10, 11], it is known that the solution for the shape of the capillary bridge formed between two flat plates is:

where,

  θ is the contact angle, and

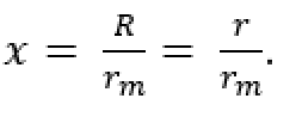
For concave capillary bridges, such as exist in the Host/tongue case, R/r_m ≥ 1.

If gravitational force is included, the form of ΔP must be re-written to include the pressure at the base of the capillary bridge, P_o, and the YL equation becomes (see, 11, for details):

Which makes the equation non-linear because of the presence of z in cylindrical coordinates (the internal pressure depends on z, since the force of gravity depends on height).  We will not analyze it, here.

     We are after the force pulling on the capillary bridge.  In [12], the force equation is derived to be:

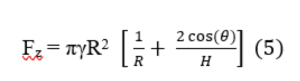
If H is much smaller than R (H<<R), as is the case, here, then the equation may be simplified to

These values are known.  γ for unstimulated saliva was measured [12] at 58.98 mN/meter, R ≈ .003 m (about 1/10 the diameter of the Host), the contact angle of unstimulated saliva is found in [13] to be about 66^o and we assume that the height of the capillary bridge is about 10 μm, which is typical of water (saliva is 99% water).  This gives a pulling force of about .333 N.

     The size of the Host received by the Communicant varies from country to country and historical period.  According to the online Catholic Encyclopedia, the diameter of the Host in Rome in 1917 was 4 cm.  80% of American Catholics receive a host made by the Cavenaugh Altar Bread Company, which uses a 1 and 3/8 inch (3.5 cm) diameter size.  Assuming that the total contact length in the mouth when the priest inserts the Host is about 1/4 of the diameter of the Host, this would imply that since the initial contact radius, R, from the previous calculations was assumed to be .3 cm at most (about 1/10 of the Host diameter) and 1/4 of the diameter of the Host is .873 cm, then the total capillary force from the extended capillary bridge (figure 2d) is about .971 N, assuming a simple linear extension of force.

     The total force on the Host during insertion is the sum of the capillary force and the downward force of S:

We may calculate this F_s, approximately, by assuming that the average mouth opening is about the size of three fingers, or about 4.5 cm.  With the mouth open and the tongue extended, this decreases the mouth opening to about 3 cm.  Assuming that S starts about halfway into the mouth or travels about 1.5 cm from the middle of the mouth opening to the tongue and that he does this placement in about 1 second, then this gives a velocity of 1.5 cm/sec.  The deceleration occurs in about .1 seconds, based on acoustical impact measurements of hand-touching-hand using free VA64 spectrum software.  The mass of the Host is about .225 grams (assuming a box of 1000 has a weight of 8 ounces, according to [15]).  This gives the force of placement on the tongue of:

So, F_total ≈ .971 N + .034 N ≈ 1.005 N

     The normal maximum 3-finger pinch strength is about 3.8 kilogram force (about 37.27 N) [16].  That much force applied to the Host would compress it, so we may assume that S’s grip strength is an order of magnitude less than this.  In a study of gripping of low-mass objects, it has been shown [16] that a quasi-linear relationship exists between weight and grip strength (although grip was higher for a lighter object owing to increased slip-guarding).  A 6 g object was pinched with .18 N force, while a 90 g object was pinched with a 1.3 N force and a 200 g object was pinched with a 2.68 N.  This data may be approximated by the polynomial:

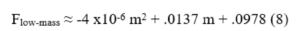
Using this approximation, the grip strength of a .225 gram object may be estimated as .100 N

     If S releases both the top and the bottom of the Host at the same speed, there is no net force generated on the Host, but in ordinary practice the thumb moves faster than the two fingers in the release creating a small upwards force on the Host:

Since no empirical data exists for the relative speed of thumb/finger release, we may simply observe that the thumb moves about 3 times faster than the fingers when the author’s pinch was released from the side of a laptop. Assuming that the mass of the thumb area is roughly the same as the mass of the bottom two fingers, this leads to the conclusion that F_thumb ≈ 3F_fingers, so that the pull-back force is roughly 3/4 of the grip strength or .075 N.  This is not enough to break the capillary force of the Host/saliva interface.

     A small air flow is induced by the movement of the hand from the tip of the tongue adding to the upward pressure.  The downward movement of the fingers creates a pressure jet [17] away from the bottom of the tongue.  The force may be calculated using the equation for a jet impacting a flat plat, with the sign changed since the force is a pulling force rather than a pushing force:

where, ρ is the density of air = 1.225 kg/m³, a is the cross-sectional area of the jet, which we take to be equivalent to the surface area of the two fingertips (3.3 cm x 2.9 cm) or .000957 m², and the pull-back velocity is approximately the same as the deposition velocity, or .015 m/sec.  Using thee values, the force of the jet is -2.69 x 10^-7 N, which is negligible.  There are other swirl effects involved when the fingers depart from the mouth, but we may assume that they are on a similar order of magnitude and may be ignored.

     The question is whether or not virions are released during the pull-back maneuver (figure 2f).  Given that the capillary force between the tongue saliva and the Host is, approximately, .971 Newtons, but the pull-back force is only, approximately, .075 N, any virions being released would have to be from the side of the capillary bridge, but assuming a height of 10 μm, and a penetration of the force of about 1 μm² projected inward (i.e., from a slight off-angle component of force) of an average viral load in saliva of 158, 489 virus copies / mL (i.e., 5.2 log₁₀ copies /  mL in virological nomenclature [18]), this gives a possible release volume of 1 x 10^-11 mL, which does not even allow for the release of a single virus copy due to thermal effects (1 x 10^-11 mL x 158,489 copies /mL = 1.58 x 10^-6 virus copies).

     The air jet force has a small horizontal component, but the force in the z direction was calculated, above at .269 μN, while the surface tension of saliva is .5898 μN for a 10 μm width of the capillary, so even if the entire air jet force were to be directed against the capillary bridge side, it would not be enough to break the surface tension and release virus copies.

     The only other possible means of virus escape while receiving on the tongue is through breathing while receiving the Host.  The subject of breathing during the reception of Communion has, at least indirectly, been studied [19].  The results indicate that there is a zero or negative (inward) pressure during a stationary open mouth (0 or -.08 millibars, depending on where it is measured). Most people, on opening their mouth draw a small amount of air inward (negative pressure), then, on thrusting out the tongue, a glottal stop likely occurs, so breathing stops, unless they specifically will themselves to breath (as [19] point out) or unless specific event-driven respiration is occurring, as in laughter. One must actively breath with one’s mouth open. The default condition is not breathing.  There is, then, almost no danger of breathing while receiving on the tongue while the mouth is open and the tongue is out, since the pressure is either zero or inwardly-directed, especially once the tongue is thrust out.

     In sum, there is almost no possibility of transmission of COVID-19 to S during contactless Communion on the tongue, even if R is infected (we will discuss the possibility of transmission from S to R, below).  The possibility of transmission due to breathing before or after the Communion event will be discussed, later.

III.  Communion on the tongue, with contact

Figure 4.  Communion on the tongue

     If contact occurs between S’s finger and R’s tongue during Communion on the tongue, virus particles may be transferred either from S to R or R to S or both (figure 4).

     The amount of virus transferred from S to R and R to S is not symmetric because the amount of virus on a hand is different than the amount in saliva on the tongue.  The typical size of the contact area between the tongue and the finger during Communion may be easily measured simply by inserting one’s finger to the tip of one’s tongue.  Depending upon contact time and amount of saliva present, either and oval or circle of saliva might be deposited.  A typical size might be a circle of .5cm in diameter.  Assuming a thickness of .1 cm, at most, this gives a total volume of saliva of .0785 mL, although [20], in testing for flu decay on hands used a 2 μL volume, so, if anything our assumptions represent an outer size limit.  According to [21], about 158,489 virus copies exist in 1 mL of saliva of an infected person, on average, so this contact involves the transfer of approximately 12,448 virus copies of SARS-COV2 onto S’s hand.  It is not known what the threshold viral load is to trigger COVID-19, but this amount is significant.

    The amount of virus on the hand varies from undetectable to a maximum comparable to sneezing directly onto one’s hand [20].  Surprisingly, there have been no studies conducted to find the average hand concentration of SARS-COV-2 on an infected person.  Most of the studies have concentrated on droplet spread.  Since the average sneeze droplet size is about 360 μm in diameter [22] and a single sneeze can contain up to 40,000 droplets.[23], a hand in direct contact with a sneeze (such as in covering ones mouth with ones hand during a sneeze) can transfer a maximum, 4/3 π (.036 cm)³ x 40,000 x 158, 489 virus copies / cm³ = 1,238,326 virus copies.  This is a very significant amount and comparable to the amount found in saliva.  This may be taken as the upper limit of virus concentration on a hand.  We assume that, in most cases, it is much lower.  The surface area of a typical adult male hand is .054 m² for the front spread hand. [24].  Assuming a uniform distribution of virus particles at 360 μm thickness (the diameter of a sneeze droplet), this gives a microfilm coating of 26,404 virions / cm³ of front hand volume.  This is comparable to the saliva concentration, as expected.  Thus, the range on the hand can be from 0 / cm³ to approximately 26,000 virions / cm³ virus particles on the entire front surface of the hand.

     How much should we expect to be on the contact area of S if S is infected and giving Communion on the tongue?  Since we have calculated the volume of a typical finger contact to be .0785 mL, this would lead to a transfer of 2041 virus particles from S to R if S is the one infected and his hand is maximally contaminated.  In addition (see, below), there could be another 2600 virions attached to the Host from S holding it before placing it on the tongue, so the total possible virion transfer is 4701 virions.   This represents an upper bound.

     It is crucial to note, however, that viral transmission from S to R via Communion on the tongue is largely irrelevant, because mouth acids and stomach acids will quickly degrade the virus.  Communion on the tongue carries, essentially, the same risk as eating take-out food.  Food does not support the growth of the virus and the best evidence is that eating food contaminated with the virus (the oral-fecal route) is not a mode of transmission of the virus.[24a]

     Thus, in all cases, there is no danger to the Communicant of catching the virus through receiving on the tongue.  Receiving on the tongue does hold a risk for S.

     If both S and R are infected, then the result is simply a swap of virus particles, with S contributing about 1/3 the number of virus particles as R.  R will transmit 12,448 virions to S and S will transmit 4701 virion to R, with the resulting exchange depositing 7,747 more virions on S’s fingers than original, with R’s amount remaining unchanged.

IV. Communion in the hand, dry contact

     Communion on the hand with dry contact (a minimum of sweat being present) can lead to different scenarios.  Obviously, if neither party has the virus, then no transmission occurs.  Since we are dealing with hand-to-hand transfer, we may assume, for sake of convenience, that both hands have the same biomechanical properties.

     There are few studies that measure how many virus particles live on the dry skin of an infected person.  The amount will depend on what virus-containing surfaces have been contacted prior to receiving Communion, degree of hand washing, etc.  Beamer, et. al, calculated the number of viruses after touching and shedding of viruses by the hands of a number of different objects over time by the formulas:

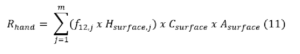
where, R_hand = rate of microbial (or viral) transfer to the hand, f_12,j = the fraction of virus transferred between the j^th surface and the hand, H_surface,j = is the contact frequency (contacts / min) between the j^th surface and the hand, C_surface = is the concentration of virus on the surface (virus / cm²), and A is the area of contact between the surface and the hand.  The transfer rate from the hand, back to surfaces is:

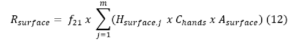
where, R_surface, is the rate of virus transfer to the surface from the hand, f₂₁ is the fraction of virus transferred from the hands to the surface, and C_hands, is the concentration of virus on the hands.[25]

     Since these number can vary wildly, a different approach is used to determine the maximum percent of virus transfer that could occur from R to S or S to R (the situation is symmetric) during dry Communion in the hand (figure 4).  The front hand surface area for an adult male is .054 m².  S places the Host in the palm of R making contact with the index and middle fingers up to the second joint of each finger, in one of the usual postures for placing the Host in the hand.  Assuming, as we did, above, that a finger is 1.5 cm in width, the tip-to-joint length of the middle finger (2nd joint) is about 6 cm and 5.5 for the index finger.  The total surface area of the two fingers is 17.25 cm² or .001725 m².  This means that 3.2% of the surface area is transferred from R to S and S to R.

     Virus particles tend to concentrate on the fingertips, the distribution of virus particles is not uniform on the palmar surface of the hand.  Julian, et. al, discovered that there was a 24 – 25% transfer of viruses between fingers and a plane of glass in their experiment in unwashed hands (the values of finger-to-glass and glass-to-finger transfer are about the same) and 15% from finger to glass and 26% from glass to finger in washed hands. [26] We assume that glass has similar properties to a dry hand, in terms of virus transfer, although this is, at best, a first approximation.  Thus, f₁₂ = f₂₁ = .24 in Beamer’s formula in transfer between unwashed hands.

     Although many scenarios of virus contact with hands are possible before the person reaches the Communion rail, we will consider one very common scenario to calculate an order of magnitude number for transfer of viruses from R to S in Communion in the hand with dry conditions.

Scenario: R sneezes into their hands and dutifully goes to the restroom to wash their hands with soap and water for 20 seconds, thus eliminating (supposedly) 99% of all virus particles.  R then goes to receive Communion

Figure 5.  Scenario 1

We, already, calculated that such a sneeze would release, approximately, 26,000 virions / cm² onto the hand.  Assuming only 1% survived cleaning, this would give a value of C_hand of, approximately, 260 virions / cm².  The contact area, A_fingers of S’s hand touching R’s hand is A_fingers = .032A_hand = 17.25 cm².  Since f₁₂ = .24 ( a 24% transfer rate), and H_surface = 1 then, assuming a single touch (j = 1) the number of virus particles transferred is f₁₂ x C_hand x A_fingers = 1076.4 virions in a perfect transfer from R’s palm to S’s finger.

     Even without making contact with R, if S is infected according to Scenario 1, merely holding the Host between two fingers and the thumb to give Communion, will expose about 10.15 cm^2 of the hand leading to about 2600 virons being deposited on the surface of the host, which might come in contact with R’s hand, in addition to the finger-to-finger contact.  This applies to Communion in the hand and Communion on the tongue.  The difference is that while the virions may be transferred from the Host to R’s hand, leading to a total possible 3676 virions during Communion in the hand, the extra 2600 virions cause no harm during Communion on the tongue because both mouth and stomach acids will degrade the virus.

     Even though the hand condition is assumed to be dry, nevertheless, there is a small microfilm layer of water vapor on the hand.  This means that the virus particles are attracted to R’s hand both by Van der Waal forces and ionic forces.  London forces are always attractive, but ionic forces may be attractive or repulsive, depending upon the charges between the two surfaces. [26].  To calculate the force of attraction of the virus particles to skin to get a rough idea of the actual amount of pulling force during the hand-to-fingers contact during dry Communion in the hand, we must use DLVO theory.

     DLVO theory (Derjaguin, Landau, Verwey and Overbeek) is a theory derived to calculate the adsorption strength (adhesive strength) of particles contacting a surface.  The total interaction energy, Φ_DLVO(h) between the two surfaces is given as the sum of the Van der Waal (London) forces, Φ_VdW(h), the electrostatic double layer (ionic) force, Φ_dl(h)  and the Born force, Φ_Born(h) [27][28]:

We assume that the surface potential is governed by a zeta potential of the form:

where, z = 5 x 10^-10 m and κ is the Debye-Huckel parameter,

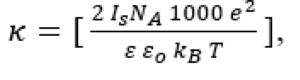
where,

where c_i is the concentration of particle I, N_A is Avogadro’s number (= 6.02 x 10²³), e is the elementary charge, ε is the dielectric constant of water, ε_o is the permittivity of free space, k_B is Boltzmann’s constant (1.38064852 × 10^-23 m² kg s^-2 K^-1) and T is the absolute temperature.

     For the contact between a roughly spherical (dodecahedron) virus particle and a flat, smooth hand (plate), the interaction energies are given by:

where, A₁₂₃ is the Hamaker contant, h is the separation distance between the virus and the hand, λ is the characteristic wavelength, σ_c is the collision diameter, and r₁ is the particle radius.  In the extended DLVO theory (XDLVO), an additional term, Φ_AB(h) is added to account for the Lewis acid/base interaction energy:

where, λ_AB is the characteristic decay length of water,

and

and θ_n is the water contact angle.

Park and Kim report that, for iron oxide particles interacting with bacteriophage MS2 ( a common test virus), the Φ_max was ~ 6 k_BT units with two minima: Φ_max ~ 3 k_BT  and  Φ_max ~ 4.15 x 10^-3 k_BT.  The maximum was found at about 70 nM separation.  This force per virion is about 2.4 x 10^-21 N M, which we assume is at least within an order of magnitude for the virion/hand interface.  This interaction was both hydrophobic and repulsive, as is common among many viruses.[26]

     To model the actual removal or deposition mechanics of virus particles during finger-to-hand contact requires a knowledge of the roughness patterns of the skin, which is beyond the scope of this study. [28a]

V. Communion of the hand, wet contact.

     It is fairly easy to calculate the number of virus particles exchanged during wet hand-to-hand contact, provided we know the viral concentration in sweat.  Unfortunately, while SARS-CoV-2 virus has been detected in sweat glands, no published values exists for its concentration in sweat. [29].  Thus, we can speculate that a sweating hand would contain more virions / cm² than in the dry scenario presented, above, but the exact amount is unknown.  A safety factor of double then amount seems prudent.  It may be possible to approximately calculate the number of virions dislodged from wet palms using the capillary bridge techniques discussed, above and mentioned in [29] once the viral concentration in sweat is known..

VI. Other possible transmission routes during Communion on the tongue or in the hand

     Aspiration can occur before and after the Communion event (barring the activation of the gag reflex while receiving, which is very rare), but that is simply regular breathing and that occurs before reception either on the tongue or in the hand.

     A typical person waits for the priest for about 30 seconds to 1 minute before receiving on the tongue or hand, if they are kneeling, and about 10 seconds while standing near the priest (not counting the time waiting in line, only when they get close enough to the priest for breathing to become significant for him). These are periods of stagnant breathing, where a breath plume is formed around the person. According to one non-peer reviewed study on the Medrxiv server, one stagnant breath event (without talking) releases .34 virions/cm^3.    The average exhalation tidal volume during quiet breathing for males or females is about .5 L or 500 cm³. Given that the average respiration rate is between 12 – 20 breaths / minute, then in 1 minute between 2040 – 3400  virions will be released, but the concentration will remain relatively small, given that the air plumes are moving outward and down and the exhaled air is being diluted by surrounding air.[30]  S is in contact with R for only about 5 seconds, so, about 1 -2 breaths are cycled.  S will expel about 340 virus particles through breathing. 

     All of this assumes that the air is stagnant and not being blown around.  Given that most churches are air-conditioned during the summer, however, stagnant air is unlikely.  In addition, the movement of the priest along the altar rail creates airflow that disperses the air plume in the case of kneeling and R’s motion in line does the same while standing in line.

    Verbalization can add up to about 2600 aerosol particles/ second, which is an order of magnitude more than the 34 – 56 particles per second for quiet breathing.[31][32][33] Thus, if S is distributing Communion to the choir, the likelihood of infection is greater than among a silent congregation.  Likewise, to say, “Body of Christ,” takes about 2 seconds, so S would release 5200 aerosol particles which might contain viruses.

VII.  Multiple mouth/hand, hand/hand contact involving S

     The figures, above, are given on a per person basis, but S often comes in contact with many people during Communion.  This makes the viral transfer a time-dependent, dynamic process.  The governing equation is equation 11:

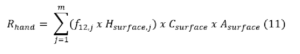
T

To calculate the time-dependent virion transfer rate on S’s hand, one may assume that the state of S (and, hence, R_hand) at time t only depends on the state of S at time t-1.  Thus, one has a situation as such:

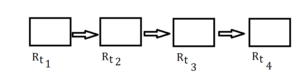
Figure 6.  Time-dependent virus transmission

   

     We assume that H is 1 (only 1 contact between S and any R).  A can take one of two values: .785 cm² for fingers/tongue contact or 17.25 cm² for fingers/hand contact.  f₁₂ seems to have an average value of 24% (.24), for fingers/hand contact, but 100% (1) for fingers/tongue contact. C can vary from 0 virions for no contact fingers/tongue Communion or no infection dry fingers/hand Communion to 1076 virions for infected dry fingers/hand contact in Scenario 1 to 2041 virions for fingers/tongue contact, to 3000 virions for wet infected fingers/hand/contact in Scenario 1 to 6240 for full sneeze fingers/hand contact to 12,448 for infected tongue/fingers contact.  Because S will both pick up virions on his hand from R’s tongue or hand and lose virions when he deposits them on R’s tongue or hand, f can take positive or negative values.  The possibilities are summarized in table 3.  We will use a + sign to indicate that the virus is present in the hand or tongue and a – to indicate that it is missing.  Likewise, we will consider transmission from R to S to be the positive direction (+ values) and transmission from S to R to be the negative direction (- values).  The word, Host, indicates the virus transfer from the viruses attached to the Host while S holds it.

Type of Contact: F=finger, T=tongue, H=hand	f	A (cm2)	C (Virions / cm2)	R (Virions Transferred to S)
F/T No Contact	1	0.785	0	0
F/H No Contact	0.24	17.25	0	0
F–/T– No Infection	1	0.785	0	0
F–/H– No Infection	0.24	17.25	0	0
F–/T+	1	0.785	158,489	12448
F+/T– Scenario 1	1	0.785	2600 + Host	-4701
F+/T+ Scenario 1	1	0.785	158,489 + Host	7747
F–/H+ Scenario 1 Dry	0.24	17.25	260	1076
F+/H– Scenario 1 Dry	0.24	17.25	260 + Host	-3676
F+/H+ Scenario 1 Dry	0.24	17.25	260 + Host	swap viruses + Host = -2600
F–/H+ Scenario 1 Wet	0.24	17.25	520	2152
F+/H– Scenario 1 Wet	0.24	17.25	520 + Host	-4752
F+/H+ Scenario 1 Wet	0.24	17.25	520 + Host	swap viruses + Host = -2600
F+/T– Sneeze	1	0.785	26000 + Host	-23010
F–/H+ Sneeze	0.24	17.25	26,000	107,640
F+/H– Sneeze	0.24	17.25	26000 + Host	-110,240
F+/H+ Sneeze	0.24	17.25	26,000	0 (swap viruses)

Table 3:  Virion Transfer Data

We omit the case where S or R have different skin moisture: Dry/Wet hand conditions, because they duplicated the results of Wet hands.  This leaves 17 conditions.

     We ran a simulation involving 200 Communions in a row by S.  To simulate the process, we generated 200 random numbers from 0 to 1 and broke them into 17 bins. Each of these bins represents one of the above scenarios,1 to 17.  We, then, took the bin values and added them sequentially, so that the virions changed from contact to contact.  The results for 4 Communion services are plotted in figure 7.  Negative values represent transfer from S to R and positive numbers represent transfer from R to S. 

 

 

 

 

 

 

 

 

 

 

 

 

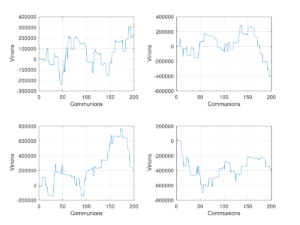
Figure 7. Simulated Virion Transfer from R to S and S to R

     Obviously, this represents the worst-case scenario, but the calculations show that the viral transfer can be significant. 

     If we assume that most people are conscientious and practice hand sanitizing, we may drop the sneeze rows, leaving 13 cases.  Likewise, the CDC has estimated that only 5% of the population has had the virus and of them, only 30% are asymptomatic carriers (we assume those with symptoms stay home or do not receive Communion).  This means that the non-zero values only occur in 1.5% of the population and the columns with zero result in no net change.  This leaves 9 plausible transfer scenarios.  If we adjust the weighting so that the non-zero values make up only 1.5 percent of the transfer in each case, we may calculate a more realistic dynamic transfer process.  The result for 4 runs is shown in figure 8.

 

 

 

 

 

 

 

 

 

 

 

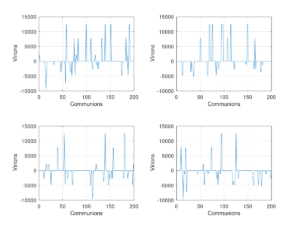
Figure 8.  Realistic Simulated Virion Transfer from R to S and S to R

     Next, we ran a simulation of 100 Masses with 200 people receiving Communion at each Mass.  The heat map shows the virus transfers (figure 9).

 

 

 

 

 

 

 

 

 

 

Figure 9.  Heat map of virus transfer for 100 Masses

     Finally, we calculated a running average for each of the 100 Masses (figure 10).

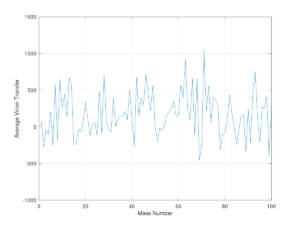
Figure 10.  Average virion transfer for each of the 100 Masses

VII. Discussion

     Simulations of worst-case and realistic Communion of 200 people were made.  We did not include aspiration from talking, which is, essentially, a constant, since S repeats, “The Body of Christ” and R repeats, “Amen”, in every case in the post-1970 Mass, while the priest says, “Corpus Domini Nostri Iesu Christi custodiat animam tuam in vitam aeternam, Amen,” in every case, while R says nothing, in the Latin Mass (making the Latin Mass very slightly safer from the standpoint of aspirations).  These statements release a small amount of virus particles (about 5200) which are quickly dispersed by the movement of the priest. 

     One may rank the transmission routes from R to S according to viral amount transferred per contact as in table 4.

Type of Contact: F=finger, T=tongue, H=hand	f	A (cm2)	C (Virions / cm2)	R (Virions Transferred to S)
F+/H– Sneeze	0.24	17.25	26000 + Host	-110,240
F+/T– Sneeze	1	0.785	26000 + Host	-23010
F+/H– Scenario 1 Wet	0.24	17.25	520 + Host	-4752
F+/T– Scenario 1	1	0.785	2600 + Host	-4701
F+/H– Scenario 1 Dry	0.24	17.25	260 + Host	-3676
F+/H+ Scenario 1 Dry	0.24	17.25	260 + Host	swap viruses + Host = -2600
F+/H+ Scenario 1 Wet	0.24	17.25	520 + Host	swap viruses + Host = -2600
F/T No Contact	1	0.785	0	0
F/H No Contact	0.24	17.25	0	0
F–/T– No Infection	1	0.785	0	0
F–/H– No Infection	0.24	17.25	0	0
F+/H+ Sneeze	0.24	17.25	26,000	0 (swap viruses)
F–/H+ Scenario 1 Dry	0.24	17.25	260	1076
F–/H+ Scenario 1 Wet	0.24	17.25	520	2152
F+/T+ Scenario 1	1	0.785	158,489 + Host	7747
F–/T+	1	0.785	158,489	12448
F–/H+ Sneeze	0.24	17.25	26,000	107,640

Table 4.  Ranking of virion transmission routes

     In the simulated realistic cases, the majority percent of virus transfer is from the communicant to the priest.  It is vital, therefore, that the priest take care when distributing Communion.  The optimum routes involve not having contact between S and R or both not having the virus in the first place.  In either case, reception in the hand or on the tongue transfers no virus particles.

     If either S or R are infected, the amount of virus transferred depends on whether it is S or R who are infected.  If S is infected, then Communion on the tongue, even with contact, is perfectly safe for R because the risk of contracting the virus from virus transferred to the mouth is minimal.  If R is infected, the safest way for S to give Communion is in the hand, because the amount of virus transferred is about 1/6 that of through Communion on the tongue with contact by S.

     Given this data, from S’s perspective, Communion on the hand is safer, while from R’s perspective, Communion on the Tongue is safer.  If the purpose is to protect R, then Communion on the tongue is safer; if the purpose is to protect S, then Communion in the hand is safer.  In general, Communion on the tongue is slightly safer in about a 2/10 vs 3/10 ratio. Table 11 summarizes these results (only dry hand Communion is considered, because wet gives the same risk, with doubled numbers, but does not change the conclusions).

Communion Type	Risk to R	Risk to S
Tongue, No Contact, No Virus	None	None
Tongue,  Contact, No Virus	None	None
Tongue, Contact, R Virus	None	12,448
Tongue, Contact, S Virus	None	None
Tongue, Contact, S, R Virus	None	7747
Hand, No Contact, No Virus	None	None
Hand,  Contact, No Virus	None	None
Hand, Contact, R Virus	None	1076
Hand, Contact, S Virus	3676	None
Hand, Contact, S, R Virus	2600	None

Table 11.  Risk Assessment to R and S

VII.  Conclusion

     Although this study had to make assumptions, since actual data to settle the issue of which transmits more virus, Communion in the hand or on the tongue is non-existent, it is hoped that the figures given in these calculations provide data that is both reasonable and within an order of magnitude of the true values.  The author hopes that the summary of results will be helpful in deciding the safest way to give Communion during the COVID-19 pandemic

Endnotes

     Each reference has an associated hyperlink taking the reader to the original article or website.